Irregular Gears
This article is kind of long! I split it into three pages.
Computer Implementations for Irregular Gears
There are two functional versions of the gear maker: the original in MATLAB, and a cleaner, leaner one in Python. I recommend the Python one.
Python
You can head over to my Github and get the source code! There's no compiled binary or anything, but if you have Python installed it shouldn't be too much fuss.
Operation is described in the readme file. Change some of the parameters at the top of main.py if you wish. Then, run main.py; you will be prompted for an image file (your input gear). Soon you'll be prompted to save your output gear as a separate image file. That's all there is to it!
This work is licensed under the Revised BSD license.
MATLAB
The original version written in MATLAB. Download it here, feel free to play around with it.

This work is licensed under a Creative Commons Attribution 3.0 Unported License.
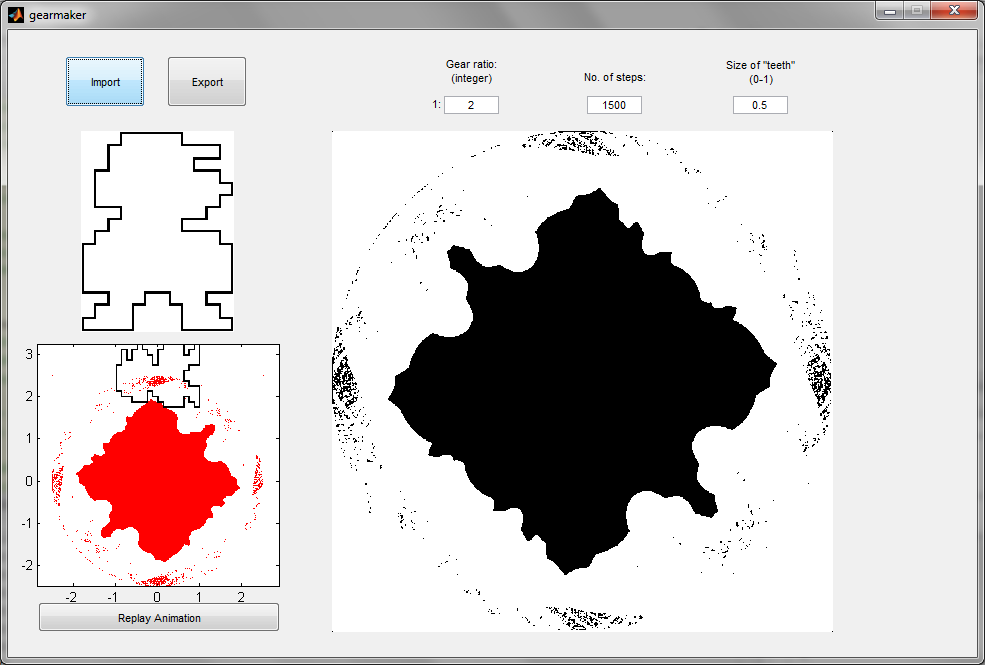
The .rar file includes two sample images and a not-totally-intuitive MATLAB GUI. If the .m and .fig files are in the same folder, you should be able to just open the .m file in MATLAB and run it. You can change the gear ratio, number of steps, and "tooth size" (how far your input gear image can spill out over the circle).
Unless you use a completely bonkers huge number of steps, the output from the program won't be perfect. It gets run through a median filter to do some denoising without messing up the edges, but there will still be speckles around it.
NOTES:
- Normal gears can be used with non-integer gear ratios because every tooth is identical. Since the entire point of this program is to facilitate ridiculous tooth shapes, it is designed to work only with integer gear ratios.
- For the input gear: points not on the perimeter of the gear won't ever affect the output gear shape. If you can use an outline-only input image, like the one shown in the GUI above, it means WAY fewer points to compute and WAY faster calculations.
- It's not fast! The GUI takes a couple seconds to run through all the steps.
- Also, the center of the input gear is assumed to be the geometric center of the image after being cropped.